Hoe meet de gps de afstand bij heuvels en bergen?
Iemand vroeg ons: als ik een steile bergwandeling maak, meet de gps dan de afstand in het platte vlak of de afstand schuin omhoog en weer naar beneden? Dezelfde vraag kun je je stellen bij een fietstocht in de bergen.
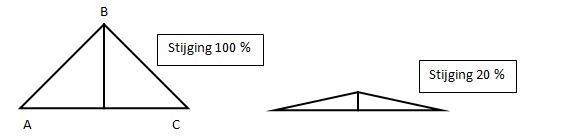
Of de vraag in een tekening: meet de gps de afstand van A naar C of de afstand va A naar B naar C? In dit geval, met een stijginghoek van 45° (ofwel 100 %):
als AC = 10 km, dan ABC = 14,14km (Pythagoras: 1, 1, √2); over de berg is dus 4,14km langer!
Nu zul je zelden zo’n sterke stijging en daling meemaken, maar het blijft interessant om te weten of je bij 20 % stijging 10km hebt afgelegd of 10,198. Verhoudingsgewijs ziet dat er uit als de rechter illustratie: wel minder spectaculair; maar fiets het maar eens omhoog, 5km lang …!
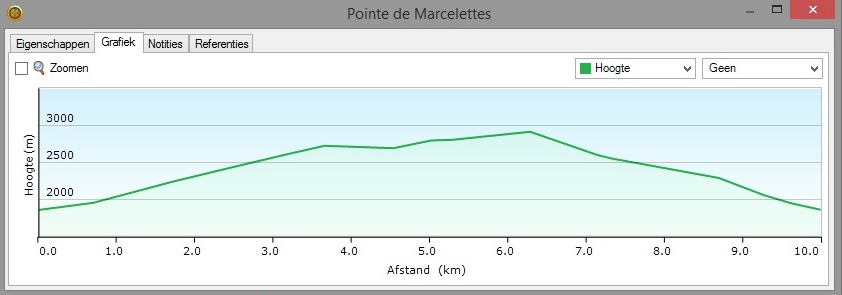
Of bij een bergwandeling in de Hautes Alpes:
Tracklengte bij een bergtocht
De tracklengte geeft aan 10 km. Is dat in een plat vlak gemeten? Of via de top? Heb je 10 km gelopen of 10,218 (bij een stijging + daling van 21%) ?
 We hadden zelf een vermoeden: de meting is in het platte vlak. Andere specialisten die we het vroegen, zeiden: we denken dat het de meting over de top is. Maar, zeiden ze, het is een vermoeden; en probeer maar eens proefondervindelijk te bewijzen wat juist is…
We hadden zelf een vermoeden: de meting is in het platte vlak. Andere specialisten die we het vroegen, zeiden: we denken dat het de meting over de top is. Maar, zeiden ze, het is een vermoeden; en probeer maar eens proefondervindelijk te bewijzen wat juist is…
Wij bedachten het volgende. Bij het Maarnse Gat, ofwel de Zanderij Maarn, is er een zeer steile trap: naar schatting bijna 450 ofwel bijna 100%. Daar moest iets op te meten zijn…
Al eerder hadden we een simpele proef bij de Lekbrug in Vi anen bedacht:
anen bedacht:
- we maakten twee waypoints pal boven elkaar, op de grond en bovenop de brug
- we bekeken het hoogteverschil – dat bleek ruim 10m te zijn
- we maakten een directe route van die twee waypoints
Vraag: hoe lang is de route? Dat bleek 0m te zijn. Ofwel: met de hoogte wordt geen rekening gehouden.
Controle, zowel beneden als boven uitgevoerd: we startten een navigatie van het ene naar het andere wpt; pal onder of pal boven het andere wpt was de Afstand tot bestemming 0 m. Elke meter die we opzij bewogen gaf een meter meer Afstand tot bestemming.
Conclusie: bij navigatie tussen twee waypoints wordt geen rekening gehouden met de hoogteverschillen.
Terug naar de proef in de Zanderij Maarn:
- onderaan de trap maakten we een wpt, startten we de trackopname en toen klommen we omhoog
- bovenaan stopten we de trackopname en maakten we een waypoint aan
- vervolgens maten we de lengte van de leuning van de trap en die was iets meer dan 40m.
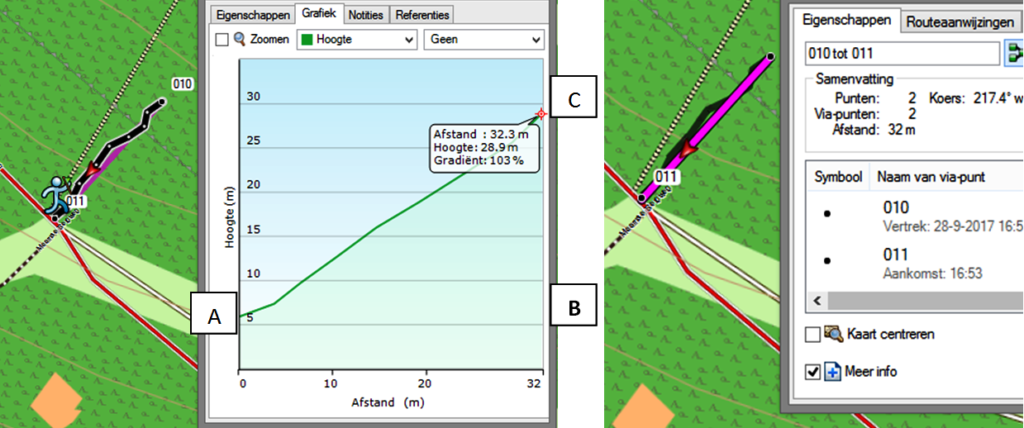
- thuis in BaseCamp bekeken we de resultaten:
1) de ietsje slingerende track was 32,3 m lang
2) de directe route tussen de 2 wpts was 32 m lang en we weten al dat die route in het platte vlak is gemeten
Conclusie:
Omdat track en route (nagenoeg) even lang zijn, zijn beide in het platte vlak gemeten.
Volgende stap: als we volgens de stelling van Pythagoras (a2 + b2 = c2) de lengte van de op de trap gelopen afstand berekenen, dan weten we de trackafstand platte vlak = 32,3m (AB) en de hoogte = 23m (BC) en dus: AC = √(AB2 + BC2) = √(1043,29 + 529) =√1572,29 = 39,7 m. De met het touw gemeten afstand van de leuning was 40 m. Met enig krediet voor de onnauwkeurigheid van een touw en de gps afwijking lijkt dit alles aardig te kloppen en tot de conclusie te leiden:
Het opnemen van een track gebeurt in een plat vlak zonder rekening te houden met de gemaakte hoogtemeters.
« Terug naar nieuwsoverzicht